Come si costruiscono

Premessa

Metodo empirico

Coordinate geografiche del luogo

Declinazione della parete

Posizionamento dello stilo

Nota sull’installazione dello stilo

Metodo con disco equatoriale

Metodo grafico

Metodo matematico

Premessa

Non pretendo qui di dare indicazioni esaurienti per il progetto di un orologio solare, esistono libri e libri sull’argomento.

Il mio solo scopo è rispondere brevemente ed esaurientemente (se possibile) alla domanda che mi viene sempre rivolta quando si parla dell’argomento: come si fa a progettare un orologio solare ?

Pertanto cercherò di descrivere brevemente i vari metodi che si possono utilizzare per la costruzione di un orologio su parete verticale, con particolari dettagli per quelli che più si prestano ad una migliore comprensione del funzionamento dell’orologio, nonché i passi preliminari indispensabili per la misura dei parametri che poi intervengono nel progetto. Si rimanda al capitolo Riferimenti per avere informazioni più esaustive.

Vorrei infine sottolineare che chiunque, anche chi non ha mai sentito parlare di meridiane, non conosce la trigonometria, non ha conoscenze anche minime di astronomia, è in grado di costruirsi la sua meridiana, utilizzando tra i tanti metodi possibili quello a lui più congeniale.

Metodo empirico

E’ anche detto da qualcuno metodo pazienza, in quanto sono necessari mesi per la sua realizzazione. D’altra parte chiunque è in grado di seguirlo, l’unica difficoltà può essere quella di tenere conto della Equazione del tempo.

Scelta la parete su cui si intende realizzare il quadrante (parete non necessariamente verticale e non necessariamente orientata a sud) si pianta nel muro uno stilo. Non è necessario che lo stilo abbia un orientamento particolare: è preferibile che sia perpendicolare rispetto al muro, ma solamente per motivi estetici, nel caso non venga alla fine sostituito da uno stilo polare.

Le dimensioni dello stilo devono essere tali da coprire con la sua ombra la zona del muro prevista per l’orologio. Può essere conveniente fare le prime prove intorno al solstizio d’estate (21 giugno) quando il sole è più alto nel cielo e si ha quindi la massima lunghezza dell’ombra.

A questo punto occorre, ad ogni ora della giornata in cui il sole illumina il muro, segnare il punto preciso del muro in cui cade l’ombra della estremità dello stilo.

Attenzione: l’ora deve essere quella solare, non quella del tempo medio che segna il nostro orologio da polso. Quindi, rifacendosi ad una tabella della Equazione del Tempo (EdT) come quella presentata precedentemente o utilizzando appositi programmi che forniscono questo dato per qualunque giorno dell’anno (ad esempio il programma Dialist’s Companion) occorre calcolare il valore della EdT nel giorno corrente e con tale dato correggere l’indicazione del nostro orologio⁵.

Ad esempio, il 26 giugno la EdT vale 2m 50s, il che significa che il sole è in ritardo di 2 minuti e 50 secondi, inoltre è in vigore l’ora legale. Questo significa che ad esempio le 12:00:00 (12 esatte) solari avverranno alle 13:02:50 (13 ore, 2 minuti e 50 secondi), le 15:00:00 avverranno alle 16:02:50 e così via.

Occorre quindi segnare la posizione dell’ombra alle 8:02:50, alle 9:02:50 ecc. segnando accanto l’ora (quella solare) della misura (7, 8 ecc.).

Si otterrà una disposizione sul muro simile a quella di Figura 19.

Per alcune ore non sarà possibile segnare l’ombra, in quanto fuori dal quadrante. Ciò non ha importanza.

Occorre ora ripetere la stessa operazione in un diverso momento dell’anno. Supponendo che la prima sia stata fatta intorno al solstizio d’estate, ripetiamo il tutto intorno al solstizio d’inverno (21 dicembre).

Aggiungendo i nuovi riferimenti sul muro, otterremo la situazione di Figura 20.

Si noti che ora alcune ore per le quali non era stato possibile segnare l’ombra sono segnate nel disegno, in quanto il sole più basso sull’orizzonte ha fatto rientrare nel quadrante l’ombra dello stilo.

Se abbiamo fatto tutto correttamente, unendo con una linea retta le coppie di punti corrispondenti alle stesse ore e prolungando verso l’alto la linea, troveremo che tutte le linee convergono nel punto C (Figura 21).

Dato poi che tutte le linee devono incontrarsi in C, possiamo anche tracciare le linee per quelle ore di cui avevamo un solo punto, unendo quel punto con C (in figura le ore 9, 10 e 16).

Abbiamo così ottenuto tutte le linee orarie del nostro orologio solare⁶.

Se volessimo aggiungere le linee diurne, dovremmo allora eseguire le misure descritte esattamente nelle date dei solstizi (21 giugno e 21 dicembre) ed unire quindi tra di loro i punti ottenuti.

Per inserire inoltre la linea degli equinozi, essendo questa sempre retta, ci è sufficiente ad uno dei due equinozi (21 marzo o 23 settembre) segnare l’ombra in due momenti qualsiasi della giornata, abbastanza lontani tra loro, ed unire quindi i due punti con una retta (Figura 22).

Il nostro orologio solare è completo.

Resta da decidere se lasciare lo stilo che abbiamo usato fino ad ora, la cui ombra segna l’ora con la sola estremità, o se sostituirlo con uno stilo polare, che segna l’ora con tutta l’ombra, essendo questa sovrapposta alle linee orarie.

Lo stilo polare del nostro quadrante è semplicemente quello che si incastra nel muro nel punto C e che finisce con l’altra estremità nello stesso punto nello spazio in cui si trovava l’estremità dello stilo provvisorio.

La Figura 23 illustra forse meglio il procedimento.

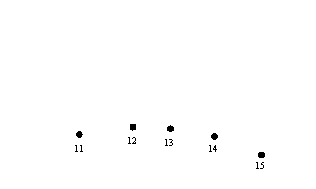
Figura 19 — Metodo empirico – passo 1

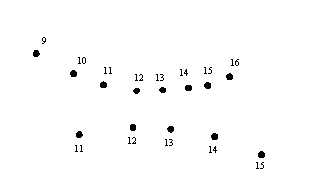
Figura 20 — Metodo empirico – passo 2

Figura 21 — Metodo empirico – passo 3

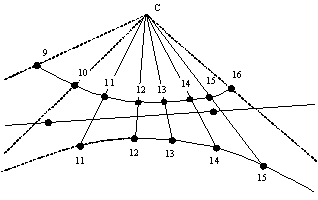
Figura 22 — Metodo empirico – passo 4

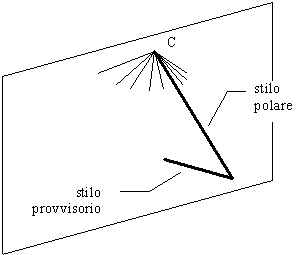
Figura 23 — Metodo empirico – passo 5 

⁵  Ricordarsi inoltre dell’eventuale ora legale !

⁶  Se non avessimo corretto l'ora con l'EdT non avremmo ottenuto un unico punto C come intersezione tra le linee orarie. Infatti in tal caso i punti non apparterrebbero ad una linea oraria bensì sarebbero due punti qualsiasi della lemniscata corrispondente, i quali non sono necessariamente allineati e possono quindi portare a tracciare delle linee assolutamente sbagliate.

Coordinate geografiche del luogo

Il primo dato indispensabile per il progetto di un orologio solare (salvo che si usi il metodo empirico) è la conoscenza delle coordinate geografiche (latitudine e longitudine) del luogo. Tale dato influisce tanto sul posizionamento dello stilo quanto sull’orientamento delle linee.

Per avere queste indicazioni è possibile seguire varie strade:

· Consultare l’Ufficio Tecnico del Comune, è possibile che vi sappiano rispondere.

· Consultare una mappa sufficientemente dettagliata della zona, ad esempio le cartine militari IGM 1:25000. Queste riportano le coordinate geografiche degli estremi del foglio, sulle quali è possibile interpolare per ottenere le coordinate del punto desiderato.

· Utilizzare il programma Google Earth che fornisce, insieme alla visualizzazione satellitare della zona cercata, anche le coordinate geografiche.

· Consultare un ricevitore GPS.

Qualunque sia il metodo, alla fine si avranno due angoli, normalmente espressi in gradi, primi d’arco (sessantesima parte di un grado) e secondi d’arco (sessantesima parte di un primo).

Ad esempio Castellamonte ha coordinate 45° 22’ 57” nord e 7° 42’ 48” est⁷. 

⁷  Da notare che i secondi, ed anche i primi, variano di molto all’interno di un territorio pur piccolo come quello di Castellamonte: l’errore comunque rientra all’interno delle tolleranze che si ottengono nella costruzione dell’orologio.

Declinazione della parete

Per declinazione della parete si intende l’orientamento della parete stessa rispetto al sud (Figura 24).

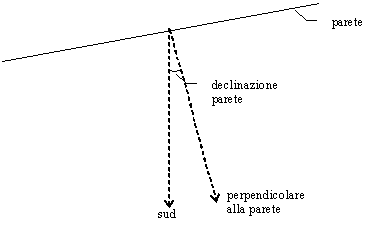
Figura 24 — Declinazione della parete

Questo dato deve essere misurato con particolare cura, in quanto influisce pesantemente sul progetto (di nuovo, il metodo empirico non richiede questa informazione).

Il metodo più preciso, ma non l’unico, ritengo sia il seguente.

Si pone un filo a piombo di fronte alla parete e si misura, su una superficie orizzontale, l'angolo che l'ombra del filo forma rispetto al muro (Figura 25). Segnare inoltre la data e l'ora esatta della misurazione.

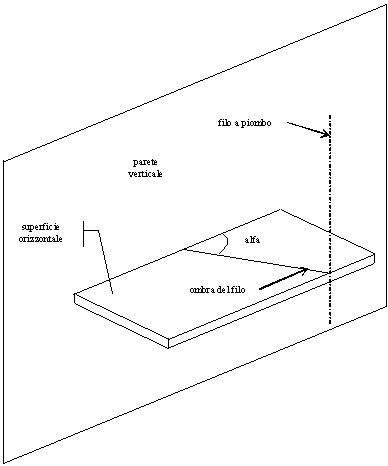
Figura 25 — Misura della declinazione della parete

Confrontare quindi l’angolo alfa misurato con l’azimut solare all’istante della misurazione (ottenibile ad esempio con il programma Dialist’s Companion) ed ottenere così lo scostamento del muro rispetto al sud, ovvero la sua declinazione.

Il risultato è nuovamente un angolo, questa volta con segno (positivo per declinazione a ovest, negativo per declinazione a est).

Si supponga ad esempio di effettuare 3 misurazioni nella giornata del 19 settembre 2005 alle ore 10:27, 13:33 e 17:48 in una località posta a latitudine 45° 22' 57" nord e longitudine 7° 42' 48" est.

In corrispondenza delle tre misure si calcola l'azimut solare.

Se si utilizzano le formule matematiche occorre risalire dal Tempo Medio dell'Europa Centrale (TMEC) al tempo vero solare locale effettuando le seguenti operazioni:

· togliere 1 ora essendo in vigore l'ora legale

· sottrarre il valore della Equazione del Tempo (in questo caso negativa, quindi il sole è in anticipo rispetto al tempo medio)

· togliere l'errore di longitudine (la località dista 7° 17' 12" cioè 7.29° dal meridiano di riferimento, corrispondenti a 4*7.29 = 29.16 minuti = 0:29:09 ore, questo numero deve essere sottratto in quanto la località è ad ovest del meridiano di riferimento, quindi il sole è in ritardo)

Alle 10:27 del TMEC si ha ad esempio che il tempo solare locale è pari a :

10:27:00 - 1:00:00 - (-0:06:11) - 0:29:09 = 9:04:02

In corrispondenza di questo tempo vero si calcola l'azimut solare⁸ che in questo caso vale –54.51° (rispetto al meridiano locale, ovvero rispetto al sud, quindi con valori negativi per sole mattutino o crescente e valori positivi per sole pomeridiano o decrescente).

In alternativa si può far fare tutti i conti al programma Dialist's Companion, facendo attenzione ad impostare correttamente le opzioni (latitudine, longitudine, fuso orario, ora legale, correzione longitudine), ed ottenere immediatamente il valore di azimut.

A questo punto si può calcolare la declinazione della parete come :

d = 90° – alfa + azimut

L'angolo alfa misurato alle 10:27 con il metodo descritto vale 12.5°, quindi la declinazione del muro vale :

90° – 12.5° + (-54.51°) = 22.99°

Effettuate alcune misure in ore e/o giorni diversi e scartati eventualmente i risultati notevolmente diversi da tutti gli altri (e quindi probabilmente affetti da errori di misura non trascurabili), si effettua la media e si utilizza il risultato finale come declinazione della parete.

In questo caso la media fornisce 23.55° ovvero 23° 33'.

Ancora più semplice è misurare la posizione dell’ombra all’ora del mezzogiorno vero locale (quindi corretto con errore di longitudine ed EdT) per cui azimut=0 : la declinazione della parete si ottiene direttamente come:

d = 90° – alfa

In alternativa a tutti questi calcoli si può utilizzare il mio programma Orologi Solari che fornisce direttamente il risultato a partire da coordinate geografiche, data e ora della misura e angolo alfa (vedi la figura 39).

Le foto di Figura 26 mostrano lo strumento che ho costruito per effettuare la misurazione della declinazione del muro secondo il metodo descritto.

Si tratta di una squadra di legno che appoggiata al muro presenta una superficie a questo perpendicolare. Una livella a bolla mi permette di posizionarla in modo orizzontale. Ad un supporto di metallo è appeso il filo a piombo la cui ombra si proietta su un foglio di carta su cui traccio la linea dell’ombra e la linea del muro, da queste successivamente misuro l’angolo alfa e, con il mio programma, calcolo la declinazione della parete.

Figura 26 — Misura della declinazione 

⁸  Per il calcolo dell'azimut occorre sapere il valore di declinazione solare il giorno della misura, lo si può ottenere da apposite tabelle o programmi.

Posizionamento dello stilo

A questo punto, avendo a disposizione tutti i dati che servono (latitudine, longitudine e declinazione) è possibile definire la posizione dello stilo.

Definiamo anzitutto le grandezze in gioco (Figura 27).

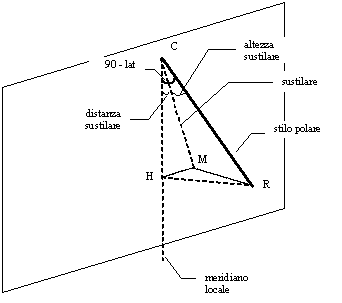
Figura 27 — Elementi del gnomone

Si definisce sustilare o substilare la proiezione ortogonale CM dello stilo sulla superficie del quadrante.

Si definisce distanza sustilare l’angolo HCM cha la sustilare CM forma con la linea del meridiano locale CH.

Si definisce altezza sustilare l’angolo MCR che lo stilo CR forma rispetto alla sua proiezione CM sul quadrante.

Come sappiamo lo stilo polare deve essere parallelo all’asse terrestre.

Per un muro verticale perfettamente orientato a sud lo stilo giace su un piano verticale perpendicolare al muro (piano del meridiano locale) e forma con questo un angolo pari a 90°-latitudine (vedi Figura 28).

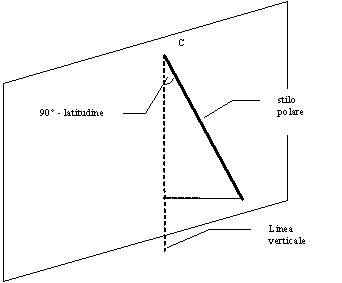
Figura 28 — Stilo su parete non declinante

Se il muro è differentemente orientato (cioè declinante) verso est o verso ovest, si immagini che lo stilo resti fermo sul piano del meridiano e che il muro ruoti verso est o verso ovest. Si hanno le due situazioni di Figura 29 e Figura 30.

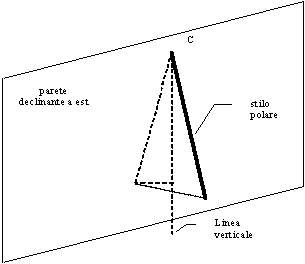
Figura 29 — Stilo su parete declinante ad est

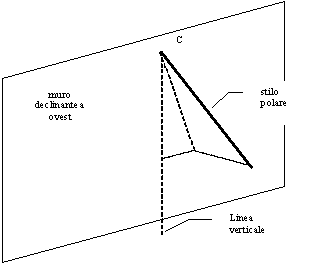
Figura 30 — Stilo su parete declinante ad ovest

L’angolo tra stilo e muro non è più quello indicato in Figura 28 e deve essere determinato in qualche modo in base a latitudine e declinazione del muro.

Riassumendo :

· per una parete esattamente esposta a sud si ha che la sustilare coincide con il meridiano locale, la distanza sustilare è quindi 0° e l’altezza sustilare vale 90°-lat (Figura 28)

· per una parete declinante a est o ad ovest il punto M si trova rispettivamente a sinistra o a destra di H (Figura 29 e Figura 30)

Un primo metodo per il posizionamento dello stilo è ancora empirico. Non richiede la conoscenza della declinazione del muro, è semplice ma poco preciso.

Si costruisca il triangolo CHR su un pezzo di cartone o comunque di materiale sottile e rigido: l’angolo HCR vale 90°-lat, l’angolo CRH lat, l’angolo CHR 90°.

Si appoggi il lato CH del triangolo sulla verticale con il vertice C posizionato nel punto del futuro incastro dello stilo.

All’ora del mezzogiorno vero locale (ore 12:00 corrette con l’errore di longitudine e con l’Equazione del Tempo) si ruoti il triangolo intorno a CH fino ad avere l’ombra del lato CR esattamente sulla verticale (meridiano locale). La posizione così trovata è tale che CR coincide con lo stilo polare⁹.

Un altro metodo è grafico, ovvero richiede di tracciare con riga e compasso delle linee sul muro in modo da ottenere graficamente il risultato ottenuto (si veda il capitolo Metodo grafico).

Un ulteriore metodo, secondo me il più preciso, richiede di eseguire alcuni calcoli trigonometrici o, ancor più semplicemente, utilizzare programmi di calcolo già disponibili. Si veda il capitolo Metodo matematico.

⁹  Questo metodo, oltre che poco preciso, è applicabile solo per pareti non troppo declinanti. Infatti più aumenta la declinazione più aumenta la lunghezza dell’assostilo e più si allontana il punto C, fino ad arrivare al caso estremo di declinazione uguale a ±90º ove l’assostilo è parallelo alla parete e sia il punto di incastro C che la linea del meridiano locale si trovano a distanza infinita. 

Nota sull’installazione dello stilo

L’installazione dello stilo sulla parete è un’operazione per nulla facile. Può essere utile a tale scopo utilizzare uno strumento simile a quello di Figura 31.

Si tratta di una tavoletta piana dotata di supporti che ne permettono il fissaggio alla parete, mantenendola perpendicolare alla parete stessa. Sulla tavoletta è poi presente un sistema per il fissaggio dello stilo, in questo caso due sbarrette dotate di viti e bulloni.

Dopo avere tracciato la sustilare e praticato il foro per murare lo stilo, si fissa il supporto alla parete mediante tasselli. I fori di fissaggio del supporto devono essere asolati in modo da poter fissare il supporto il più precisamente possibile sulla sustilare.

Si fissa quindi lo stilo al supporto e si misurano accuratamente tutti i parametri dello stilo (altezza sustilare, ortostilo, assostilo). Verificare inoltre la perpendicolarità della tavoletta alla parete, correggerla se necessario spessorando opportunamente i punti di appoggio.

Quando si è sicuri della posizione si può procedere a cementare lo stilo e chiudere il foro.

Al termine dell’operazione, smontato il supporto, conviene verificare la verticale CH e, se necessario, ritracciarla.

Figura 31 — Posizionamento e fissaggio dello stilo

Metodo con disco equatoriale

Questo metodo è di non molto facile realizzazione ma ha secondo me il vantaggio di chiarire ulteriormente il meccanismo di funzionamento dell’orologio solare, infatti viene simulato il percorso che i raggi solari compiono nel segnare con l’ombra l’ora durante il giorno.

In Figura 17 si è visto come con un orologio solare equatoriale si possa spiegare il funzionamento di un orologio solare su parete verticale.

Sfruttando questo concetto, una volta posizionato correttamente l'assostilo sul muro, è possibile tracciare le linee orarie e volendo anche le linee diurne senza ulteriori calcoli o complessi processi grafici.

È però necessario anzitutto costruire uno strumento come quello di Figura 32.

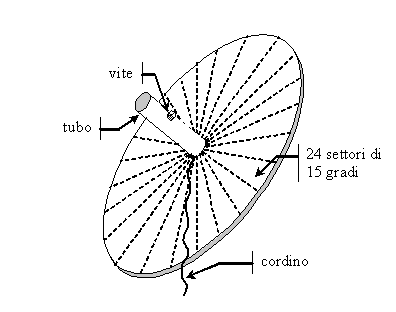
Figura 32 — Disco equatoriale ausiliario

Si tratta ancora di un disco, la cui superficie è divisa in 24 parti di 15˚ ognuna. Al centro del disco, anziché lo stilo perpendicolare come in un orologio equatoriale, viene posizionato un tubo perpendicolare con diametro interno sufficiente a farvi passare lo stilo che è stato fissato alla parete. Una vite consente di fissare il tubo sullo stilo nella posizione desiderata. Inoltre al tubo deve essere fissato un cordino che permetterà di ricavare la posizione delle linee orarie sulla parete.

Fissato correttamente l'assostilo alla parete, si infila il tubicino del disco equatoriale sullo stilo e si fissa quindi in uno dei seguenti modi:

1. Orologio che indica il tempo locale (senza correzione della longitudine - Figura 33)

Si tende il cordino in modo che resti parallelo al disco ed arrivi a toccare la linea verticale tracciata dal punto C (che è la linea oraria del mezzogiorno locale), si ruota il disco in modo che una delle linee tracciate sulla sua faccia coincida con il cordino e si stringe quindi la vite per fissare il disco allo stilo. La linea coincidente con il cordino è quella delle ore 12, in successione a destra e a sinistra si hanno le ore successive e precedenti.

In alternativa (ma mi sembra meno preciso) è possibile posizionare il disco con l’aiuto di una livella in modo tale che la linea che unisce le ore 6 con le ore 18 sia orizzontale. 

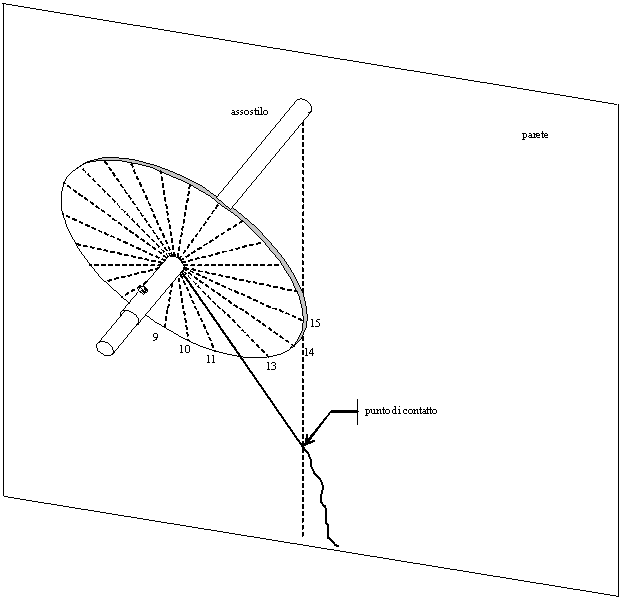
Figura 33 — Posizionamento del disco equatoriale ausiliario (senza correzione longitudine)

2. Orologio che indica il tempo del fuso orario (con correzione della longitudine - Figura 34)

Occorre anzitutto tracciare in un settore del disco lo scostamento che deriva dalla longitudine del luogo: calcolata la differenza in gradi tra la longitudine locale e quella del fuso orario, la si riporta su un settore del disco come indicato in Figura 34.

Quindi si procede come al punto 1. ma in questo caso il cordino dovrà coincidere con la linea appena tracciata, mentre sul muro il cordino dovrà sempre toccare le linea verticale da C (che è ancora il mezzogiorno locale ma non quello del fuso, quest'ultimo coincide con la successiva linea da 15º).

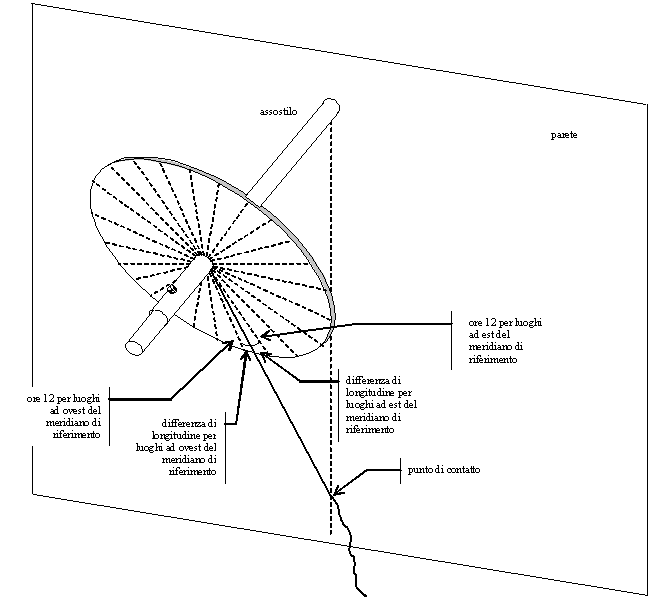
Figura 34 — Posizionamento del disco equatoriale ausiliario (con correzione longitudine)

Quando si traccia sul disco la linea corrispondente alla differenza di longitudine in gradi, per sapere se questa debba essere disposta a sinistra o a destra della linea da 15˚, si tenga presente che :

· per una località ad ovest del meridiano di riferimento del fuso (è il caso ad esempio di Torino) sulla parete il mezzogiorno del fuso rimane a sinistra della linea verticale (mezzogiorno locale)

· per una località ad est del meridiano di riferimento del fuso (è il caso ad esempio di Bari) sulla parete il mezzogiorno del fuso rimane a destra della linea verticale (mezzogiorno locale)

Ora che il disco è saldamente fissato allo stilo si procede, in entrambi i casi, a spostare il cordino di volta in volta sulle linee a 15˚ tracciate sulla sua superficie, mantenendolo sempre parallelo ed aderente al disco, e segnando quindi sulla parete il punto di incontro cordino-muro.

Questi punti saranno quelli che, uniti al centro C, ci forniranno le linee orarie.

Nel caso 1. avremo la linea delle 12 coincidente con la verticale da C (che è il meridiano locale).

Nel caso 2. avremo il mezzogiorno a sinistra della verticale per i luoghi ad ovest del meridiano del fuso, a destra per quelli ad est del meridiano del fuso.

In Figura 35 è indicata la situazione per una località ad ovest del meridiano del fuso (es. Torino).

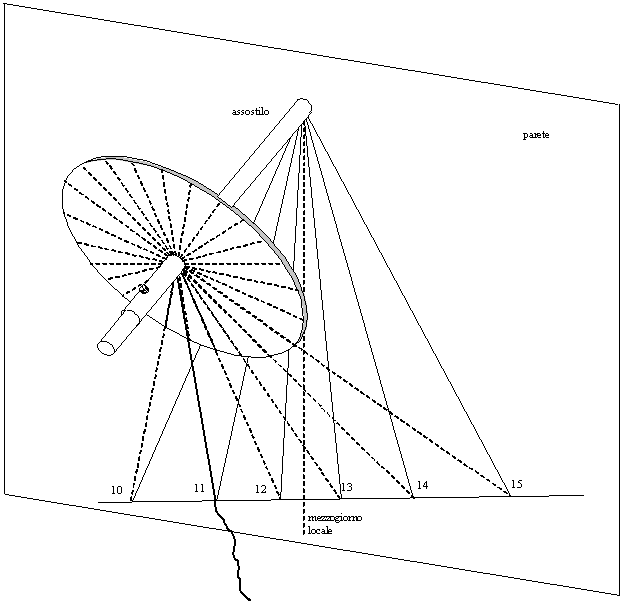
Figura 35 — Tracciamento delle linee orarie con disco equatoriale ausiliario

In pratica quello che stiamo facendo è simulare con il cordino il percorso dei raggi solari agli equinozi (raggi paralleli all'equatore terrestre) e cercare il punto in cui questi segnano sul muro l'ombra dello stilo. È necessario quindi che il cordino possa ruotare intorno al tubo centrale del disco, pur mantenendo sempre lo stesso punto di ancoraggio rispetto allo stilo, in modo che, quando teso, esso tracci una retta che passa per il centro (sempre lo stesso) dello stilo.

Si noti inoltre che i punti tracciati sono quelli toccati agli equinozi dall'ombra del punto dello stilo a cui abbiamo fissato il cordino, quindi se questo è il punto che ci segnalerà le stagioni abbiamo anche ottenuto la linea diurna degli equinozi. Dovendo questa essere una linea retta, dovremmo trovarci tutti i punti segnati sulla parete allineati su una retta.

Volendo poi tracciare anche le linee diurne dei solstizi, è necessario costruire un nuovo attrezzo, in modo che il cordino teso possa simulare anche i raggi di sole inclinati di ± 23˚ 26' rispetto all'equatore terrestre (e quindi rispetto al nostro disco).

In pratica si tratta ancora di un tubo da fissare sullo stilo, al quale è connesso un cordino ed un indicatore graduato che permette di inclinare il cordino rispetto al disco equatoriale della quantità di gradi desiderata, in particolare di ±23.5° (Figura 36).

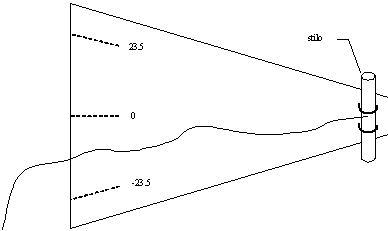
Figura 36 — Strumento per il tracciamento delle linee diurne

Per ogni linea oraria tracciata, si posiziona lo strumento in modo tale che il cordino, mantenuto teso e parallelo al piano dello strumento, tocchi la linea stessa. Inclinando il cordino nelle tre posizioni indicate si ottiene l’intersezione della linea oraria con le tre linee diurne (solstiziali ed equinoziali). Il punto che indicherà sul quadrante la stagione è il punto di ancoraggio del cordino allo stilo.

È importante infine osservare che questo metodo funziona per qualunque parete piana, anche non verticale, purché lo stilo sia stato correttamente posizionato. È così possibile in modo abbastanza semplice disegnare un orologio solare su una superficie piana comunque orientata.

Metodo grafico

Questo metodo soffre del potenziale accumulo di errori che possono facilmente essere commessi durante il lungo processo di disegnazione.

Peraltro il disegno risultante ha un fascino particolare e sarebbe degno di essere lasciato sul muro anche ad orologio terminato.

Si inizia con il calcolo del posizionamento dello stilo. Come abbiamo visto, per una parete esposta perfettamente a sud questo si troverebbe su un piano verticale perpendicolare alla parete e formerebbe con questa un angolo pari a 90° - latitudine. Per una parete declinante occorre invece calcolare distanza ed altezza sustilare.

Il processo consiste in pratica nel rovesciamento dei triangoli CHR e HMR di Figura 27 sul piano del quadrante.

Si inizia (Figura 37) con una linea orizzontale AB posta al di sotto di C, centro delle linee orarie e punto di fissaggio dell’assostilo.

Figura 37 — Ricerca grafica di distanza ed altezza sustilare

Si traccia la linea CR’ tale che l’angolo HR’C sia uguale alla latitudine φ del luogo. Il segmento CR’ corrisponde alla lunghezza dello stilo. R’ è a destra di C per declinazioni a ponente, a sinistra di C per declinazioni a oriente.

Da H si traccia la linea HR” tale che l’angolo R”HR’ sia uguale al complemento della declinazione del muro, cioè 90°- d.

Da H si traccia un arco di cerchio con raggio HR’ che incrocerà HR” in R”. Da R” si traccia la perpendicolare ad AB individuando così il punto M.

La retta CM è la sustilare cercata, mentre R”M corrisponde alla lunghezza dell’ortostilo.

Il triangolo gnomonico sarà quindi composto dai lati CR’ (assostilo), CM (sustilare) e RM (ortostilo).

Resta ora da tracciare le linee orarie.

Il processo assomiglia molto a quanto visto per il metodo con equatoriale, in effetti si tratta di proiettare sul piano del quadrante la equatoriale correttamente disposta e da questa derivare le linee orarie.

Questo procedimento può essere trovato nei riferimenti in appendice, in particolare nel libro di René Rohr “Meridiane”.

Anzitutto ribaltiamo sul piano il triangolo CMR di fig. 27: dal punto M della sustilare CM trovata in fig. 37 si traccia la perpendicolare MR’” (Figura 38) e con centro nello stesso punto M si traccia l’arco di cerchio di raggio MR” fino ad incontrare la retta MR’” in R’”. Il triangolo CMR’” è il triangolo CMR di fig. 27.

Figura 38 — Tracciamento grafico delle linee orarie

Si traccia quindi da R’” la perpendicolare a CR’” fino ad incontrare la sustilare CM in E; da questo punto E si traccia la perpendicolare ST alla sustilare CM. Questa retta è la equinoziale e corrisponde alla linea orizzontale di fig. 35.

Si deve ora ribaltare finalmente l’equatoriale sul piano del quadrante: con centro in E si traccia l’arco di cerchio con raggio ER’” fino ad incontrare la sustilare in O. Da questo si traccia un cerchio di raggio arbitrario. Individuato sulla verticale CH il punto d di intersezione con la ST, si traccia la retta dO. Si divide quindi la circonferenza in spicchi di 15° ognuno partendo dalla retta dO.

Prolungando i raggi così trovati fino ad intersecare la retta ST, si trovano i punti c, e, f ecc. e da questi si tracciano le linee orarie Cc, Cd … Cm. La retta Cd corrisponde alle ore 12 locali.

Dividendo il cerchio in spicchi di 7.5° si possono tracciare le linee alle mezz’ore.

Se si vuole che l’orologio segni il tempo del fuso orario di riferimento anziché l’ora vera locale, si fa corrispondere la retta Od, invece che a 0°, all’errore in gradi tra la località ed il meridiano di riferimento (esattamente come in Figura 34). In tal modo tutti i raggi del cerchio ruotano di questo valore angolare e di conseguenza si spostano i punti c, d ecc. Ovviamente in tal caso la linea Cd corrisponde ancora alle ore 12 locali ma non alle 12 del fuso di riferimento.

Metodo matematico

È il metodo più preciso per il tracciamento sul quadrante delle linee che compongono l'orologio solare ma è anche quello che meno permette la comprensione del suo funzionamento.

Applicando formule trigonometriche (vedere il libro di René Rohr “Meridiane” oppure “The British Sundial Society Glossary”) ed avendo a disposizione i valori di latitudine e longitudine del luogo e declinazione della parete, è possibile calcolare la posizione delle linee orarie e delle linee diurne.

Se una volta i calcoli potevano essere lunghi e laboriosi, oggi, con un PC ed un foglio elettronico a disposizione, diventa tutto molto più facile e veloce.

Per chi comunque non vuole o non sa applicare direttamente le formule, esistono numerosi programmi di calcolo anche freeware  che non solo effettuano tutti i calcoli, ma sovente offrono anche una presentazione grafica del risultato, molto utile per avere una idea preliminare della forma che il quadrante assumerà e determinarne quindi l'ingombro sulla parete.

Sul mio sito, all’indirizzo http://digilander.libero.it/orologi.solari/download, è disponibile gratuitamente un programma che ho chiamato, con molta fantasia, Orologi Solari che permette il progetto di:

· orologi orizzontali

· orologi verticali declinanti

· orologi equatoriali

· orologi polari

· orologi analemmatici.

L’orologio può indicare l’ora locale o quella di un qualsiasi fuso orario.

Sul quadrante si possono tracciare le ore francesi, italiche, babilonesi e temporali.

E’ inoltre possibile tracciare la lemniscata sul mezzogiorno o su tutte le linee.

Contiene inoltre alcuni strumenti utili che sono raramente disponibili in altri programmi:

· calcolo della declinazione della parete

· calcolo della illuminazione della parete nel corso dell’anno

· simulazione dell’ombra nel corso della giornata e durante l’anno

Un help in linea, oltre ad un help contestuale, aiutano nella comprensione e nell’uso del programma.

Il programma di setup installa inoltre uno screen saver : dopo aver progettato il vostro orologio potete utilizzarlo per visualizzare in tempo reale la posizione dell’ombra sul vostro quadrante (ovviamente solo in condizioni di illuminazione, quindi con sole sopra l’orizzonte e quadrante illuminato).

Per meglio vedere le caratteristiche del programma, consultare il file di help Orologi Solari Help.chm.

Programma Orologi Solari 

Torna  alla pagina
Come funzionano

Home

Vai alla pagina
Immagini

Scarica tutte le pagine in PDF

aggiornato il venerdì 06 marzo 2015