Orologi solari

How they work

Orologi solari

The earth as a sundial

It is well known that the earth rotates around its own axis and it performs a complete rotation in 24 hours. Moreover it orbits around the sun performing a complete revolution in one year (365 days) and following an orbit that is slightly elliptical (Fig. 10).

Now let's imagine that the only equatorial disc is left and that the earth axis is a real phisical element (Fig 11).

Sun rays light up the equatorial disc and the earth axis casts its shadow on the disc.

While the earth rotates around its axis, the shadow moves on the disc: in 24 hours one earth rotation is completed, the shadow has covered the complete circonference and in 24 hours it reaches the original position.

Now let's imagine that the equatorial disc is divided into 24 equal sectors, each of them 15 degrees wide (Fig. 12).

During the day the shadow that is cast by the earth axis goes all over the 24 sectors, each sector in one hour.

If we now mark each line on the disc with the corresponding hour, then we obtain a sun dial (that in this ideal case will work for all the 24 hours day).

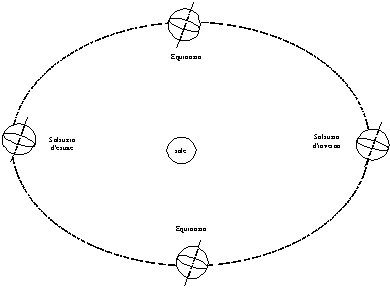
Fig. 10 — Earth revolution around the sun

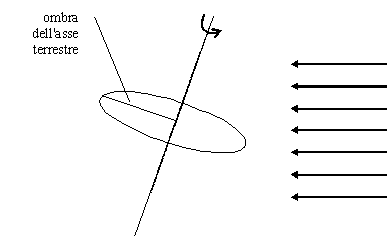
Fig. 11 — Earth as a sundial (1) ("ombra" = "shadow")

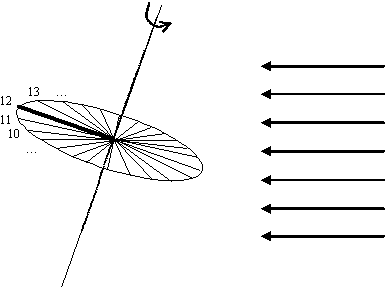
Fig. 12 — Earth as a sundial (2)

Equatorial or Equinoxial dials

Let's now imagine that we take the above equatorial disc, together with its axis, and we move it to the earth surface, keeping fixed its original orientation (i.e. disc parallel to the equator, axis parallel to the earth axes).

As the sun is at a distance that is much larger than the earth dimensions, this movement does not change the behaviour we have just described and the disc will still correctly show the time.

We can so manufacture a true phisical disc, divide it in 24 equal sectors on both faces and put an orthogonal axis through its center. Let's position the disc in the correct way : disc parallel to the equator, axis parallel to the earth axis.

This is the simplest type of sundial taht is called equatorial or equinoxial.

It is worthy to note that the earth axis is not orthogonal to the plan that includes the earth orbit (the ecliptic plan) and it has an inclination of about 23˚ 26' .

For this reason the sun rays during the year reach the earth with an angle that changes month to month, and because of that we experience what we call seasons.

As a consequence on the equatorial dial :

in winter sun rays light up the lower part of the disc (with an angle between 0˚ at the equinox and -23˚ 26' at the winter solstice) : the lower face of the dial shows the time (Fig. 13)
at the equinoxes sun rays are orthogonal to the axis and parallel to the disc : the dial hardly shows the time as all the disc is in the shade (Fig. 14)
in summer sun rays light up the upper part of the disc (with an angle between 0˚ at the equinox and +23˚ 26' at the summer solstice) : the upper face of the dial shows the time (Fig. 15)

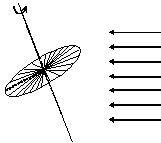
Fig. 13 — Equatorial dial at winter solstice

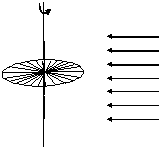
Fig. 14 — Equatorial dial at equinoxes

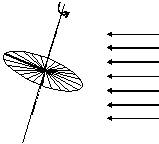
Fig. 15 — Equatorial dial at summer solstice

The advantages of this type of dial are :

the extreme simplicity
the possibility of reading the time from dawn to sunset

The drawbacks are :

the difficulty to read the time at the equinox (sun rays parallel to the disc) and in winter time (reading from the lower face)
the space needed for the installation of the disc, it is more usually installed in an open space such as a garden

How to position the equatorial dial ?
It depends on the latitude φ of the place.

With respect to the horizontal plan, the disc has to be inclined an angle equal to (90º - φ) and the axis (style or gnomon) an angle equal to φ. The axis should lie in the north-south direction (see Fig. 16)..

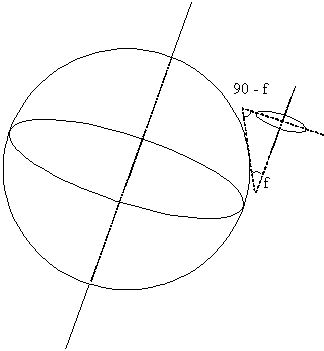
Fig. 16 — Equatorial dial set-up

Sundials on generic planar surfaces

We can now proceed starting from our model of a simple equatorial sundial and introduce some changes.

Let's take an equatorial dial that has been correctly set up as explained in the previous paragraph and let's put a vertical plan that intersects both the disc and the axis (Fig. 17).

The shadow that the axis (that is our style) casts on the disc continues on the plan as far as to reach the intersection point between the plan and the axis.

As the sun moves in the sky, the shadow on the disc moves 15 degrees each hour, and the shadow on the plan moves accordingly.

It is worthy to note that we have set-up a plan without defining its orientation with respect to the south direction nor its position with respect to a horizontal surface. It can be easily understood that whichever is the orientation of the plan the style shadow will always be a straigth line that moves according to time. This shadow can so be used to show the hours during the day (the only problem being how to practically design line hours on such a plan).

It should also be noted that the style shadow will always go through the point where the style intersects the plan, and so will have to do the hour lines to be traced on the plan.

The dial we have just described is a plan sun dial with a polar style and french hour lines.

Depending on the orientation of the plan there are the following special cases :

1. plan is horizontal => horizontal dial

2. plan is vertical => vertical declining dial

3. plan is orthogonal to the polar style => equatorial dial

4. plan is parallel to the style => polar dial

In the following chapter we will see some of the possible procedures that can be used for the design of this sun dial..

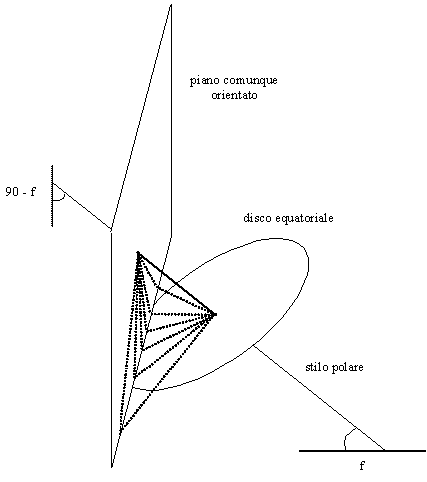
Fig. 17 — Sun dial on a generic planar surface

Fig. 18 — Vertical sun dial with a large west declination (165° W)

Go to the page
How to read them (in depth)

Home

Go to the page
How to build them

Download the PDF booklet (in Italian)

updated on venerdì 06 marzo 2015